Introduction

As a part of this article, we delve into the paradigm of Chain of Though reasoning in Large Language Models. The aim is to highlight the importance of this idea and summarize the main research in this area. The blog should provide enough context for the reader in the field of AI to understand the basic concepts and think about the potential research ideas addressing the limitations of the current models.

Chain of thought Reasoning

Chain of thought (CoT) refers to manifesting the human thought process in large language models by endowing language models with the ability to generate a chain of thought - a coherent series of intermediate reasoning steps.

It is hypothesized that CoT prompting helps LLMs to tackle complex arithmetic, commonsense and symbolic reasoning tasks. The following demonstration highlights this improvement.

COT

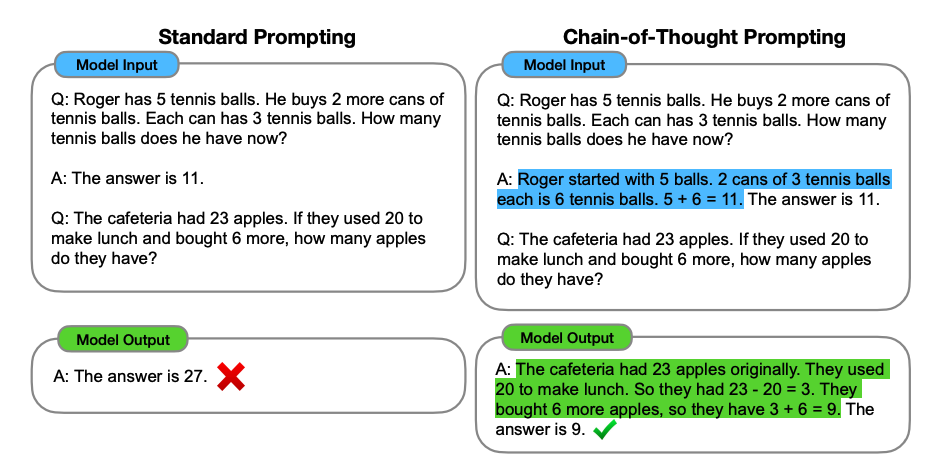
However, there are some limitations with this paradigm of reasoning with the current models.

Small models are unable to improve with CoT prompting. LLMs with more than 100B parameters show performance gains with CoT.
The performance improvements are larger with larger models. In other words, the benefits of CoT scale with the size of the models.
Sometimes the models arrive at the correct answers with the wrong reasoning. The errors have been classified as
- Calculation error - LLMs are probabilistic models, predicting what token occurs next. So when an LLM tries to do \(3* 25* 8 =\), it does not really calculate the answer but probabilistically guesses the answer which is the next token. This highlights a fundamental limitation in the current architectures of LLMs.
- Symbol mapping error - When there are too many variables involved, LLMs sometimes mix up the variables and arrive at the wrong answer. Again, the problem arises from the fundamental architecture flaw highlighted in the previous point.
- Other than these major errors, the models also have semnatic understanding problems, missing steps, incoherent chain of thought errors

Large Language Models are Human-level prompt engineers

The motivation of this paper is as follows -

Human effort in prompt engineering - Crafting effective prompts for LLMs is time-consuming and requires significant human expertise.
Optimization challenge - Primpts greatly influence LLM performance, but users often lack insight into how to optimize them for specific tasks.
Scalability - As LLMs grow in size and capabilities, manuallt designing prompts becomes less deasible for a wide range of applications.
Automating promtp design - There is a growing need to automate the prompt engineering process to enhance LLM usability and performance.
Real-world impact - Applications in diverse domains (e.g., AI chatbots, automated content generation) can benefit from optimized and automated prompts.

This work promposes an Automatic Prompt Engineer (APE) - asystem that automates prompt generationg and selection for Large Language Models. This task is treated as a program synthesis task wherein the input-output pairs (natural language questions and answers) are given to the APE, and it has to generate the instruction needed to generate these pairs.

In essence, the APE is trying to learn the prompts generated by humans. The framework is as follows -

Instruction Generation. An LLM is used as an ingeerence model where the “instruction candidates” are generated based on a small set of input-output demonstrations

Example: The input to APE is of the form -

Input 1 - Forward generation technique

”””

I gave a friend an instruction and five inputs. The friend read the instruction and wrote an output for every one of the inputs. Here are the input-output pairs

Input: [ ] Output: [ ]

Input: [ ] Output: [ ]

…

The instruction was <COMPLETE>

””””

Input 2 - Reverse generation technique

”””

I instructed my friend to <INSERT>

The friend read the instructions and wrote an output for every one of the inptus. Here are the input-output pairs:

Input: [ ] Output: [ ]

Input: [ ] Output: [ ]

…

”””
Scoring Instructions. Evaluate each instruction by computing a score that reflects how well the instruction guides the target LLM for the task. This is simply the confidence score associated with the log likelihoods of token generation. The authors consider a moving average score considering the probabilities for a window of tokens.

They also consider an execution accuracy - the success of an instruction by checking if the model produces the correct output (0-1 loss). However, this cannot. be used for all kinds of instructions.

The top \(k\)-percentile prompts are selected and the rest are discarded.
LLM as Resampling Model. They apply an Iterative Monte search method to resample more prompts. The LLM generates semnatically similar instructions variants to improve the top-performing candidates.

Once the prompts are generated, the moving average scores are generated for each of the prompts and the better scoring prompts are selected again.

Can APE be used to guide LLMs?

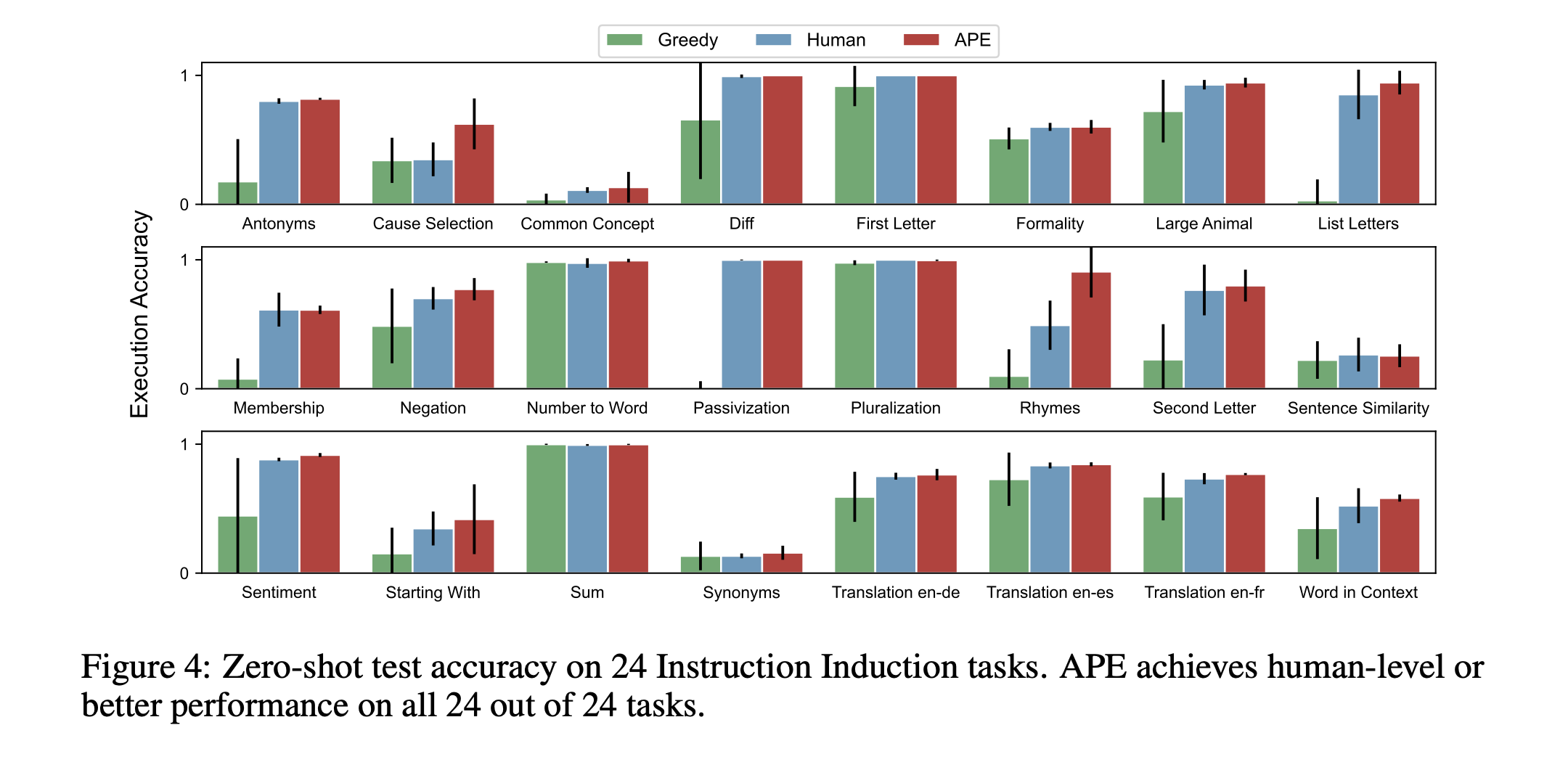
Although this is a very simple example, the work shows potential in taking such framework forward to work with more complex applications.

Another interesting approach is to not generate the prompts from scratch, but to help humans design better prompts. Essentially, augment with context from humans to generate better prompts. On the flipside, RLHF can be used to improve these APE.

Tree of Thoughts

The early Language Models were limited by their token-level, left-to-right decision making. However, some tasks require exploration, stratefic lookahead, planning, and backtracking. The vanilla architecture does not support such mechanisms.

Framework

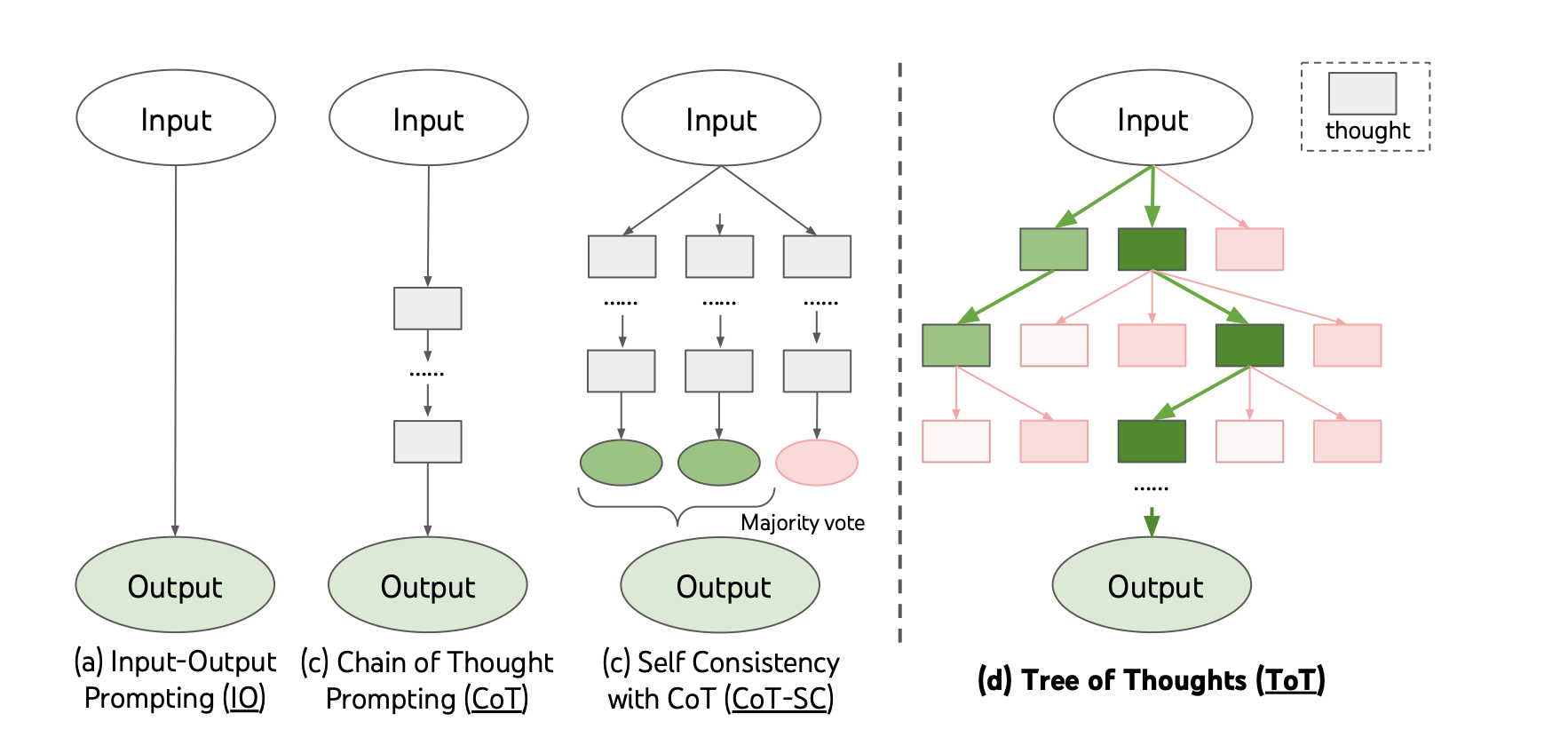
Mathematically, these models are depicted as

Input output programming - \(y \sim p_\theta^{IO}(y \vert x)\)
Chain

Theoretically, the model seems promising. However, there are some intricate details that need to be figured out -

How to decompose the porcess into steps
How to generate the potential thoughts from each state
- Need to be small enough so LMs can generate promising and diverse samples
- Big enough so LMs can evaluate the difference contributing to the results
How to heuristically evaluate each state
How to navigate through the generated tree

Thought decomposition

Method 1 - Direct Prompting

The prompts themselves can ask the LM to segment the problem into multiple problems. Due to the voting mechanism, LM generates multiple possibilities for an answer and chooses the best model. This works better when thought space is rich and i.i.d samples lead to diversity.

Method 2 - Backtracking

Propose thoughts sequentially using a “propose prompt”. When the thought space is constrained, this works better - proposing different thoughts in the same context avoids duplication.

State Evaluator

There are two strategies to evaluate each generated state

Value each state independently, where a value prompt reasons about the state \(s\) to generate a scalar value \(v\). This value is very context dependent.
Vote across states by deliberately comparing different states in \(S\) in a vote prompt.

Search Algorithm

BFS is helpful when the tree depth is limited and the initial thought steps can be evaluated and pruned to a small set
DFS explores longer trees well - subtrees are pruned to trade exploration for exploitation.
More advanced approaches such as \(A^*\) and MCTS are left to future work in the paper.

An interesting summary of all thought paradigms - Demytifying Chains, Trees, and Graphs of Thoughts.

On Second Thought, Let’s Not Think Step by Step! Bias and Toxicity in Zero-Shot Reasoning

We have seen how chain of thought improves problem solving capabilities. However, in some cases, CoT actually causes issues -

The authors explore such effects in the paper. They consider

Least-to-most prompting enables complex reasoning in Large Language Models

The key motivators for the paper are as follows -

Given a new task

In the prior works, CoT reasoning has been effective for many tasks but struggled with “Easy-to-hard generalization”. Inspired from educational philosophies, the model is implemented by few-show ptompting in 2 stages - decomposition stage and subproblem solving stage.

Decomposition stage - The problem is divided into subtasks once before solving
Subsequent solving stage - Solve the subsequent problems one by one.

The key difference from CoT prompting is that CoT starts each sub-problem from scratch and is unable to build from previous reasoning. This behaviour is depicted using the symbolic manipulation task in the paper - The performance of CoT progressively decreases as the length of the list increases.

This method of prompting achieves significantly better results borrowing the context from the previous subproblems to arrive at the final answer.

However, decomposition thoughts don’t generalize across domains. This limitation mainly shows up for math problems where the subproblems need to be correctly decomposed to solve the original problem.

Chain of Thoughtlessness

CoT prompting sounds too good to be true. The paper aims to test this paradigm rigorously to verify the claims. The paper also tries to identify the difference between complex reasoning and pattern matching - What seems like “complex reasoning” may just be a case of pattern matching?

Consider the chain of thought reasoning -

How specific do the prompt examples have to be to the original problem?
How generalizable are these prompts or how specific do they need ot be?
How much human effort is needed to craft prompts for each problem subclass?

Furthermore, there are issues with the test domains as well. For example, GSM8K

They are non scalable - problem instances cannot be scaled
The problems are static and be easily found in the training data

The main point the paper is trying to address the question - “Is it really possible to teach an LLM how to solve a generalizable problem?”. To test this claim, the authors choose “Blocks world” as the problem domain - given an initial and end configuration, output a series of steps to reach the end configuration from the initial configuration.

They perform the following experiments

Zero shot CoT - Simply append “Let’s think step by step” to the prompts.
Progression proof - Specific to planning problems. Each example’s steps describe the init state, action taken, reason of the action and the final step.

They see that zero-shot CoT achieves insignificant performance gains from zero-shot prompting. The progression proof CoT achieves a lower performance - this may be due to overfitting to the training examples. The LLM fails to learn the universal block algorithm (break the tower and put everything back) even with multiple version of CoT prompting. The authors chose a planning domain on purpose because these problems can be scaled up very well.

The authors just wanted to highlight that there is a need for more rigorous testing. One might argue that planning problems are way out of domain of LLMs. So, the authors test the findings with commonly tested problems, and they find similar trends.

Chain of Thought without prompting

Prompting techniques, while effective, often encode task-specific human priors, thereby making it difficult to assess a language model’s intrinsic reasoning abilities. Ideally, a language model should be able to reason independently and provide the optimal response, without requiring humans to tweak the prompts or refine repeatedly if the initial response is unsatisfactory. Model-tuning can be expensive and requires a substantial amount of supervised data. In this work, we explore a different perspective and ask: Can LLMs reason effectively without prompting? And to what extent can they reason? We find that, perhaps surprisingly, there exists a task-agnostic way to elicit CoT reasoning from pre-trained LLMs by simply altering the decoding procedure. Figure 1 illustrates this phenomenon: given a reasoning question, the LLM generates a wrong answer via the standard greedy decoding path, yet alternative top-𝑘 token inspection unveiled inherent CoT paths (e.g., decoding paths 2 and 4), which accurately resolved the query. This decoding modification bypasses prompting and is entirely unsupervised without the need for model tuning.

Why can’t LLMs reason if we only consider greedy decoding path?

Large Language Models are Zero-shot reasoners

Large Language Model Reasoning